Array Implementation of Queue
- Implement the core operations of Queue efficiently (array-based).
- Explain why an efficient array-based implementation of Queue can logically be viewed as a circular data structure.
We want to implement the Queue interface using an array as an internal data storage.
Exercise Think about how to implement a queue using an array such that the core operations are constant time. Assume the array is sufficiently large.
| Operation | How? | Time |
|---|---|---|
enqueue | $\Omicron(1)$ | |
dequeue | $\Omicron(1)$ | |
front | $\Omicron(1)$ | |
empty | $\Omicron(1)$ |
Solution
Initialize two variables front and back to zero.
When you equeue, add to the back. Use the back variable to index into the array. Then increment it.
When you are asked for front element, simply return arr[front].
When you dequeue, simply increment front.
Since you remove from the "front" of the array, then there will be empty positions at the front. So, when the back variable reached the end of the array, it can wrap around it and write to the (actual) "front" of the array, to positions that were removed earlier.
This gives rise to a logical view of array being a circular data structure.
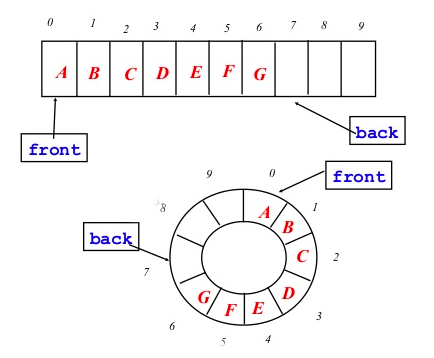
You can also dynamically grow the array when back reaches front.
| Operation | How? | Time |
|---|---|---|
enqueue | data[back] = value and back = ++back % length | $\Omicron(1)$ |
dequeue | front = (front + 1) % length | $\Omicron(1)$ |
front | return arr[front] | $\Omicron(1)$ |
empty | check if numElement == 0 | $\Omicron(1)$ |
The % length is a trick we use to reset the index when it reaches the length of the array. We could rewrite it as
font = front + 1;
if (front == length) {
front = 0;
}
The example above replaces front = (front + 1) % length. The same idea can be applied to updating back variable.
Resources
- Data structures: Array implementation of Queue on YouTube.
- Using an Array to represent a Circular Queue on YouTube.