Delete Operation

Suppose we have a linked list with $n$ elements (nodes) and we want to delete an element at a given index $k$. This means we remove the $k^{th}$ node from the list. After deletion we have $n - 1$ elements:

• The node which was at index $k - 1$ before the deletion will remain at that index after the deletion.
• The nodes at index $k + i$ for $i \in [1, n-1-k ]$ before the deletion will be at index $k+ j$ after the deletion for $j \in [0, n-2-k]$.

For example, we have a linked list with four nodes at indices 0, 1, 2, and 3.

We will delete the node at index 2:

Exercise Complete the implementation of delete which removes a node at the given index.

public void delete(int index) {
	// TODO Implement me!
}

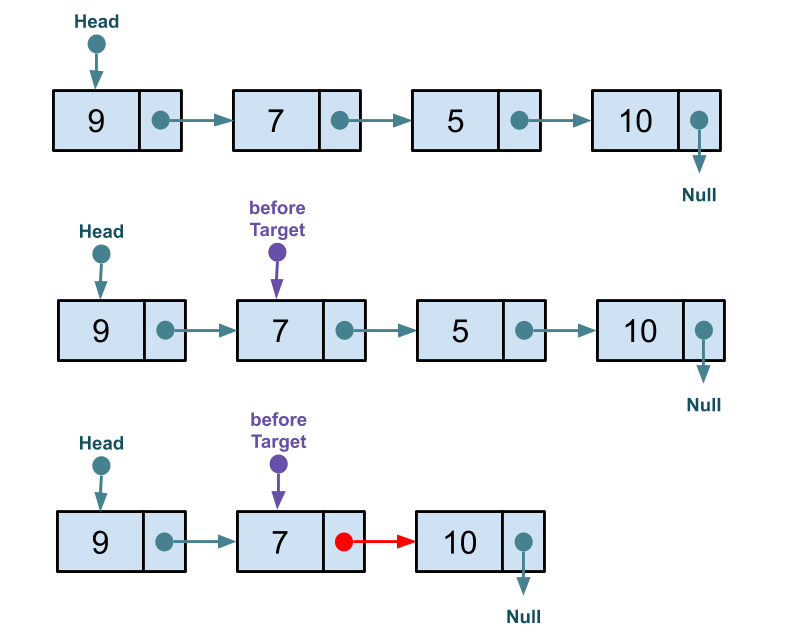
Hint: Use the following visualization as guidance.

public void delete(int index) {
  Node<T> beforeTarget = head;
  for(int counter = 0; counter < index - 1; counter++) {
    beforeTarget = beforeTarget.next;
  }

  beforeTarget.next = beforeTarget.next.next;
}