Bubble Sort: The Code

Here is how we have implemented bubble sort:

/**
 * The Bubble Sort algorithm with the optimized "quick" break to exit
 * if the array is sorted.
 *
 * @param <T> The type being sorted.
 */
public final class BubbleSort<T extends Comparable<T>>
    implements SortingAlgorithm<T> {

  // is a less than b?
  private boolean less(T a, T b) {
    return a.compareTo(b) < 0;
  }

  @Override
  public void sort(IndexedList<T> indexedList) {
    boolean swapped;
    for (int i = indexedList.length() - 1; i > 0; i--) {
      swapped = false;
      for (int j = 0; j < i; j++) {
        if (less(indexedList.get(j + 1), indexedList.get(j))) {
          swap(indexedList, j, j + 1);
          swapped = true;
        }
      }
      if (!swapped) {
        return;
      }
    }
  }

  // Pre: i & j are valid indices.
  // Post: elements at i & j are swapped.
  private void swap(IndexedList<T> indexedList, int i, int j) {
    T t = indexedList.get(i);
    indexedList.put(i, indexedList.get(j));
    indexedList.put(j, t);
  }

  @Override
  public String name() {
    return "Bubble Sort";
  }
}

Please run the bubble sort code in "debug" mode for the following sequence of values:

$$ 14, 10, 23, 34, 6, 17, 50, 14 $$

You can use the unit test in SortingAlgorithmTest for this purpose.

Exercise Complete the following trace table. As you fill out the table, think about the role of the boolean variable swapped as it is used in the code above.

Solution

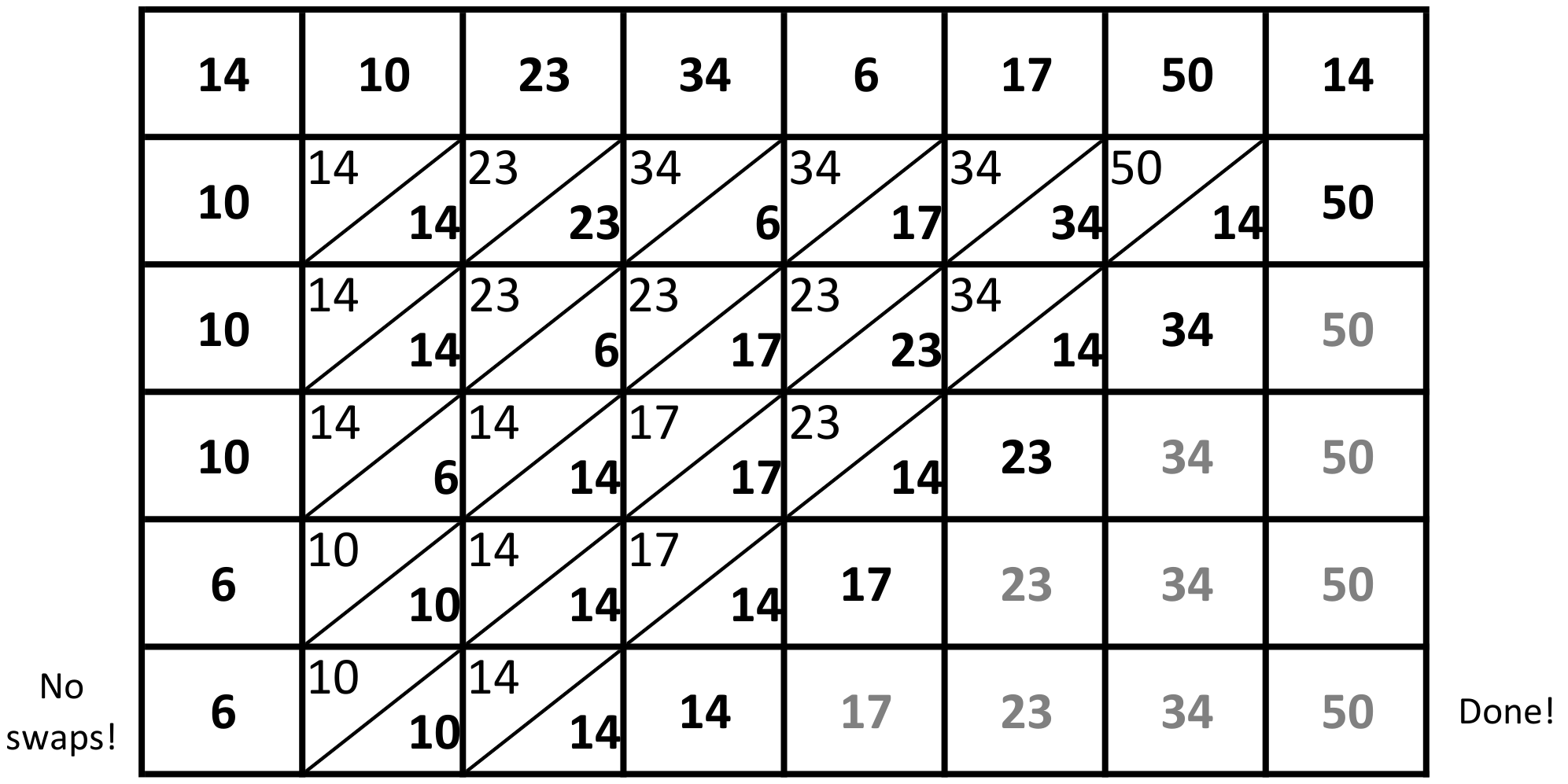
The swapped variable would allow us to stop early if no swaps were made in a full pass of the outer loop. When no swap is made in a complete pass, the items are already in sorted order. We call this the "stop early if no swaps" optimization!